Learning Constrained Dynamics with Gauss Principle adhering Gaussian Processes
2020
Conference Paper
ics
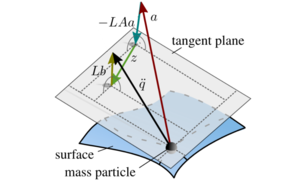
The identification of the constrained dynamics of mechanical systems is often challenging. Learning methods promise to ease an analytical analysis, but require considerable amounts of data for training. We propose to combine insights from analytical mechanics with Gaussian process regression to improve the model's data efficiency and constraint integrity. The result is a Gaussian process model that incorporates a priori constraint knowledge such that its predictions adhere to Gauss' principle of least constraint. In return, predictions of the system's acceleration naturally respect potentially non-ideal (non-)holonomic equality constraints. As corollary results, our model enables to infer the acceleration of the unconstrained system from data of the constrained system and enables knowledge transfer between differing constraint configurations.
| Author(s): | A. René Geist and Sebastian Trimpe |
| Book Title: | Proceedings of the 2nd Conference on Learning for Dynamics and Control |
| Volume: | 120 |
| Pages: | 225--234 |
| Year: | 2020 |
| Month: | June |
| Series: | Proceedings of Machine Learning Research (PMLR) |
| Editors: | Bayen, Alexandre M. and Jadbabaie, Ali and Pappas, George and Parrilo, Pablo A. and Recht, Benjamin and Tomlin, Claire and Zeilinger, Melanie |
| Publisher: | PMLR |
| Department(s): | Intelligent Control Systems |
| Bibtex Type: | Conference Paper (inproceedings) |
| Paper Type: | Conference |
| Event Name: | 2nd Annual Conference on Learning for Dynamics and Control (L4DC) |
| Event Place: | The Cloud |
| State: | Published |
| URL: | http://proceedings.mlr.press/v120/geist20a.html |
| Links: |
Proceedings of Machine Learning Research
|
|
BibTex @inproceedings{gaussprinciple2020geist,
title = {Learning Constrained Dynamics with Gauss Principle adhering Gaussian Processes},
author = {Geist, A. René and Trimpe, Sebastian},
booktitle = {Proceedings of the 2nd Conference on Learning for Dynamics and Control},
volume = {120},
pages = {225--234},
series = {Proceedings of Machine Learning Research (PMLR)},
editors = {Bayen, Alexandre M. and Jadbabaie, Ali and Pappas, George and Parrilo, Pablo A. and Recht, Benjamin and Tomlin, Claire and Zeilinger, Melanie},
publisher = {PMLR},
month = jun,
year = {2020},
doi = {},
url = {http://proceedings.mlr.press/v120/geist20a.html},
month_numeric = {6}
}
|
|